Misalkan  adalah bilangan real positif. Buktikan bahwa
adalah bilangan real positif. Buktikan bahwa
Bukti 1:
Kita punya
Tetapi, dengan ketaksamaan GM-AM, kita juga punya
dan dengan cara yang sama diperoleh
Jadi
Bukti 2:
Perhatikan bahwa
dan dengan cara yang sama diperoleh
Bukti 3:
Kita punya
dan dengan cara serupa diperoleh
Misalkan  ,
,  , dan
, dan 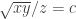 , maka
, maka  , dan yang akan dibuktikan adalah
, dan yang akan dibuktikan adalah  . Setelah menyamakan penyebut, ketaksamaan tersebut menjadi
. Setelah menyamakan penyebut, ketaksamaan tersebut menjadi 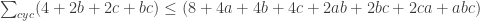 yang ekuivalen dengan
yang ekuivalen dengan  , yang jelas benar dengan ketaksamaan GM-AM.
, yang jelas benar dengan ketaksamaan GM-AM.
0 komentar:
Posting Komentar