Barisan bilangan real  memenuhi
memenuhi  ,
, 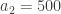 ,
, 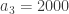 , dan juga
, dan juga 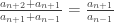 untuk
untuk  . Buktikan bahwa semua bilangan di barisan ini adalah bilangan asli dan buktikan bahwa
. Buktikan bahwa semua bilangan di barisan ini adalah bilangan asli dan buktikan bahwa  habis dibagi
habis dibagi  .
.
Bukti 1:
Dari hubungan rekursif yang diberikan, diperoleh  , maka
, maka  , sehingga
, sehingga  . Dari persamaan terakhir ini dan
. Dari persamaan terakhir ini dan  , maka diperoleh bahwa
, maka diperoleh bahwa 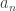 selalu berbentuk
selalu berbentuk  , untuk bilangan bulat
, untuk bilangan bulat 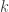 dan
dan 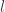 . Misalkan
. Misalkan  untuk
untuk  .
.
Kita akan membuktikan dengan induksi bahwa  . Perhatikan bahwa
. Perhatikan bahwa 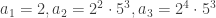 menyebabkan
menyebabkan  . Karena
. Karena  , maka
, maka  . Andaikan
. Andaikan  untuk
untuk 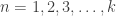 . Maka
. Maka  , sehingga bukti kita selesai. Dengan cara yang sama,
, sehingga bukti kita selesai. Dengan cara yang sama, 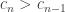 untuk semua
untuk semua  . Jadi
. Jadi  dan
dan  adalah bilangan cacah, sehingga
adalah bilangan cacah, sehingga 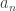 pasti bilangan asli.
pasti bilangan asli.
Telah dibuktikan dengan induksi di atas bahwa  untuk semua
untuk semua  . Akibatnya
. Akibatnya  . Maka
. Maka  pasti habis dibagi
pasti habis dibagi  .
.
Bukti 2:
Dengan cara seperti di atas, diperoleh  . Tidak ada suku yang nilainya 0, maka kita bisa tulis persamaan tadi menjadi
. Tidak ada suku yang nilainya 0, maka kita bisa tulis persamaan tadi menjadi  . Jadi nilai
. Jadi nilai  konstan, yaitu sama dengan
konstan, yaitu sama dengan  . Jadi
. Jadi 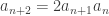 , sehingga jelas bahwa semua suku pada barisan itu adalah bilangan asli.
, sehingga jelas bahwa semua suku pada barisan itu adalah bilangan asli.
Perhatikan juga bahwa  , sehingga
, sehingga  adalah bilangan genap. Tetapi
adalah bilangan genap. Tetapi  . Ke-2000 bilangan yang dikalikan tersebut semuanya adalah bilangan genap, sehingga
. Ke-2000 bilangan yang dikalikan tersebut semuanya adalah bilangan genap, sehingga  habis dibagi
habis dibagi 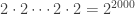 .
.
0 komentar:
Posting Komentar