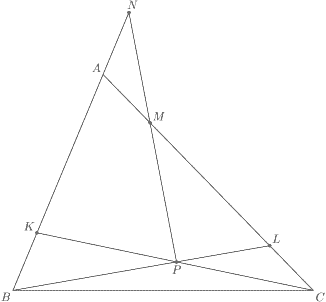
Misalkan titik  terletak pada sisi
terletak pada sisi 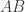 dan titik
dan titik 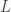 terletak pada sisi
terletak pada sisi dari segitiga
dari segitiga 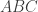 sedemikian sehingga
sedemikian sehingga  . Garis
. Garis 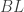 dan
dan 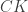 berpotongan di titik
berpotongan di titik 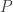 . Garis yang melalui titik
. Garis yang melalui titik 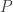 dan sejajar dengan garis bagi sudut
dan sejajar dengan garis bagi sudut 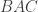 memotong garis
memotong garis  di titik
di titik 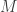 . Buktikan bahwa
. Buktikan bahwa 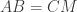 .
.
Bukti 1:
Misalkan garis yang melalui titik 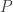 dan sejajar dengan garis bagi sudut
dan sejajar dengan garis bagi sudut 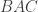 memotong garis
memotong garis 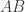 di titik
di titik 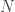 . Kita akan membuktikan bahwa
. Kita akan membuktikan bahwa 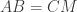 dan
dan  . Sekarang, semua pernyataan simetris terhadap
. Sekarang, semua pernyataan simetris terhadap 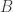 dan
dan 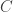 (artinya
(artinya 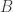 dan
dan 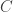 dapat dipertukarkan), maka tanpa mengurangi keumuman anggaplah
dapat dipertukarkan), maka tanpa mengurangi keumuman anggaplah  .
.
Perhatikan bahwa  dan
dan  . Maka
. Maka  , akibatnya
, akibatnya  .
.
Dengan dalil Menelaus pada segitiga  dan garis transversal
dan garis transversal 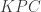 diperoleh
diperoleh  . Karena
. Karena  , maka
, maka  .
.
Dengan dalil Menelaus pada segitiga  dan garis transversal
dan garis transversal  diperoleh
diperoleh  . Karena
. Karena  (telah dibuktikan di atas), maka
(telah dibuktikan di atas), maka 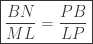 .
.
Gabungkan kedua hasil di atas, maka kita mendapat bahwa  , atau
, atau  . Karena
. Karena  ,
,  , maka
, maka  . Persamaan terakhir ini ekuivalen dengan
. Persamaan terakhir ini ekuivalen dengan
 . Karena
. Karena  , maka
, maka  sehingga
sehingga  .
.
Jadi 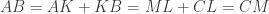 dan
dan  . Dengan ini bukti kita sudah selesai.
. Dengan ini bukti kita sudah selesai.
Bukti 2:
Buat titik  sedemikian sehingga
sedemikian sehingga 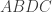 adalah jajar genjang. Misalkan titik
adalah jajar genjang. Misalkan titik  adalah perpotongan garis
adalah perpotongan garis 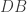 dan garis
dan garis 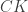 , misalkan juga titik
, misalkan juga titik 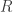 adalah perpotongan garis
adalah perpotongan garis 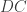 dengan garis
dengan garis 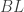 .
.
Karena 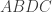 adalah jajar genjang, maka garis
adalah jajar genjang, maka garis  sejajar dengan garis
sejajar dengan garis  . Jadi segitiga
. Jadi segitiga  sebangun dengan segitiga
sebangun dengan segitiga 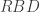 .
.
Perhatikan bahwa segitiga  sebangun dengan segitiga
sebangun dengan segitiga 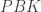 sehingga
sehingga  . Kita juga tahu bahwa
. Kita juga tahu bahwa  , maka
, maka  . Karena segitiga
. Karena segitiga  sebangun dengan segitiga
sebangun dengan segitiga 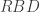 , maka
, maka  , sehingga
, sehingga  . Jadi, menurut teorema garis bagi,
. Jadi, menurut teorema garis bagi,  adalah garis bagi dari sudut
adalah garis bagi dari sudut  .
.
Karena 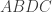 adalah jajar genjang, maka garis bagi dari sudut
adalah jajar genjang, maka garis bagi dari sudut  sejajar dengan garis bagi sudut
sejajar dengan garis bagi sudut  . Jadi
. Jadi  sejajar dengan garis bagi sudut
sejajar dengan garis bagi sudut  . Akibatnya
. Akibatnya 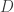 ,
, 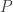 , dan
, dan 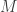 segaris. Misalkan
segaris. Misalkan 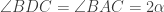 . Perhatikan bahwa
. Perhatikan bahwa 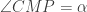 dan
dan  , maka
, maka  . Tetapi
. Tetapi 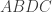 adalah jajar genjang sehingga
adalah jajar genjang sehingga 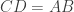 , akibatnya
, akibatnya  . Bukti kita selesai.
. Bukti kita selesai.
0 komentar:
Posting Komentar